Fill the interior of a silhouette where lines.
category: code [glöplog]
If all you have to start with is the bitmap and no information about further restrictions there is no 100% reliable way to extract the edges and/or their directions anyway because one cannot decide whether some small region or line is separate or not as it might got lost due to quantization.
Won´t be a problem for painting all interior areas as the outer boundary is always determinable, but proper even-odd-style painting is tough.
One possible approach: Outside is considered as having colour 0.
First fill all subareas which are directly attached to the outside of the polygon with color 1.
Then fill all subareas neighbouring areas with color 1 with color 2.
Then all subareas neighbouring ones with color 2 with color 3, and so on until no uncoloured subarea is left. Areas with odd colour are black, those with even colour are white.
Hard part is making this robust against quantization artifacts, e.g. by starting with the subareas with most known neighbouring pixels first and in case of subareas with more than one neighbouring colour determine their colouring state according to the one which is neighbouring (even or odd) most of its edges.
However, if you draw the outlines yourself you may detect the aliasing case by drawing the lines with additive blending, thus while reading one pixel of the polyline you immediately know whether this pixel is part of a single edge or was drawn additive by more than one edge.
This should re-enable using a scanline-on-off approach: toggle the black/white fill state on every pixel with odd draw count but keep it on every even count (including 0).
Won´t be a problem for painting all interior areas as the outer boundary is always determinable, but proper even-odd-style painting is tough.
One possible approach: Outside is considered as having colour 0.
First fill all subareas which are directly attached to the outside of the polygon with color 1.
Then fill all subareas neighbouring areas with color 1 with color 2.
Then all subareas neighbouring ones with color 2 with color 3, and so on until no uncoloured subarea is left. Areas with odd colour are black, those with even colour are white.
Hard part is making this robust against quantization artifacts, e.g. by starting with the subareas with most known neighbouring pixels first and in case of subareas with more than one neighbouring colour determine their colouring state according to the one which is neighbouring (even or odd) most of its edges.
However, if you draw the outlines yourself you may detect the aliasing case by drawing the lines with additive blending, thus while reading one pixel of the polyline you immediately know whether this pixel is part of a single edge or was drawn additive by more than one edge.
This should re-enable using a scanline-on-off approach: toggle the black/white fill state on every pixel with odd draw count but keep it on every even count (including 0).
At a first look at your picture it looks like a simple xor filler or eor filler, like they are used widely on the C64 Amiga and so on..
I think some people already pointed that out here.
However that is just working if you really draw the outlines by yourself, taking care that only one pixel per x step is drawn on every edge.
like this (just only one pixel per x step for an edge):
01000
00100
00000
00010
00001
and !!not!! (with several y pixels one over another for the same x on the edge):
01000
00100
00100
00010
00001
Then you would go over the whole picture like this, where picture helds values of 0 or 1:
for (int x = 0; x < pictureWidth; ++x) {
int xor = 0;
for (int y = 0; y < pictureHeight; ++y) {
int onoff = picture[x + y*pictureWidth];
xor ^= onoff;
picture[x + y*pictureWidth] = onoff;
}
}
That's the very basics of an xor filler. If you paint the edges you also have to xor the pixels while painting the edges.
I think T$ and some others already pointed to "somehow" the same solution. (Odd/Even counters, xor and so on)
Perhaps this helps, too..
I think some people already pointed that out here.
However that is just working if you really draw the outlines by yourself, taking care that only one pixel per x step is drawn on every edge.
like this (just only one pixel per x step for an edge):
01000
00100
00000
00010
00001
and !!not!! (with several y pixels one over another for the same x on the edge):
01000
00100
00100
00010
00001
Then you would go over the whole picture like this, where picture helds values of 0 or 1:
for (int x = 0; x < pictureWidth; ++x) {
int xor = 0;
for (int y = 0; y < pictureHeight; ++y) {
int onoff = picture[x + y*pictureWidth];
xor ^= onoff;
picture[x + y*pictureWidth] = onoff;
}
}
That's the very basics of an xor filler. If you paint the edges you also have to xor the pixels while painting the edges.
I think T$ and some others already pointed to "somehow" the same solution. (Odd/Even counters, xor and so on)
Perhaps this helps, too..
The last line must be: "picture[x + y*pictureWidth] = xor;" of course :)..
If you got the vertices and edges and a triangle rasterizer at hand you can try the “stencil buffer technique” for drawing arbitrary polygons.
—
Create a point P somewhere and draw triangles using this common point and the two vertices of each edge. For each pixel in each triangle count up a value corresponding to that pixel in a separate stencil buffer.
When you are done with all the edges, fill all the pixels that got odd values in the stencil buffer. This should give a fill with even odd fill rule.
—
Try to draw it on paper first to see if you got it right. The algorithm is also described in the OpenGL Red Book. And if you got the edge directions you can also do a nonzero fill rule.
How to extract the polygon from an image is another hard problem though.
—
Create a point P somewhere and draw triangles using this common point and the two vertices of each edge. For each pixel in each triangle count up a value corresponding to that pixel in a separate stencil buffer.
When you are done with all the edges, fill all the pixels that got odd values in the stencil buffer. This should give a fill with even odd fill rule.
—
Try to draw it on paper first to see if you got it right. The algorithm is also described in the OpenGL Red Book. And if you got the edge directions you can also do a nonzero fill rule.
How to extract the polygon from an image is another hard problem though.
Code:
uint8* I; // image data
int w, h; // image size
int totals[256], insides[256]; // counts for each region
// Recursive floodfill.
void floodfill(int x, int y, int c) {
I[y*w + x] = c;
if (x+1<w && I[y*w + (x+1)] == 0xFF) { floodfill(x+1, y, c); }
if (x-1>=0 && I[y*w + (x-1)] == 0xFF) { floodfill(x-1, y, c); }
if (y+1<h && I[(y+1)*w + x] == 0xFF) { floodfill(x, y+1, c); }
if (y-1>=0 && I[(y-1)*w + x] == 0xFF) { floodfill(x, y-1, c); }
}
int main(void) {
I = image_load("in.png", &w, &h); // pixels: 0xFF=empty, 0=boundary
// Fill each empty region with a different color.
int region = 1;
for (int y=0; y<h; y++) for (int x=0; x<w; x++) {
if (I[y*w + x] == 0xFF) { floodfill(x, y, region); region++; }
}
// Shoot rays for each pixel. Find out if the number of crossings is odd.
for (int y=0; y<h; y++) for (int x=0; x<w; x++) {
int r = I[y*w + x];
if (r == 0) continue; // boundary
for (int i=0; i<4; i++) {
int count=0, X=x, Y=y, c=r;
int dx = "2011"[i] - '1', dy = "1102"[i] - '1'; // four directions
for (;;) {
if (X==0 || X==w-1 || Y==0 || Y==h-1) break; // outside
if (I[Y*w + X] != c) { c = I[Y*w + X]; count++; } // color change
X += dx; Y += dy; // step
}
// int dx = rnd32()&1 ? 1 : -1, dy = rnd32()&1 ? 1 : -1; // random walk
// uint32 xbias = rnd32();
// for (;;) {
// if (X==0 || X==w-1 || Y==0 || Y==h-1) break;
// if (I[Y*w + X] != c) { c = I[Y*w + X]; count++; }
// if (rnd32() < xbias) { X += dx; } else { Y += dy; }
// }
totals[r]++;
insides[r] += count/2 & 1; // edge crossings = color changes / 2
}
}
// Count the number of "inside" results.
for (int y=0; y<h; y++) for (int x=0; x<w; x++) {
u32 r = I[y*w + x];
if (r != 0) { I[y*w + x] = insides[r]*2 > totals[r] ? 0xA0 : 0xFF; }
}
image_save("out.png", I, w, h);
}
- Find empty regions using floodfill.
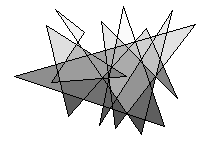
- From every pixel, walk in four directions and count edge crossings (color changes / 2). Odd = inside.

- Count the number of "inside" results in every region. If it's more than 50%, the whole region is inside.
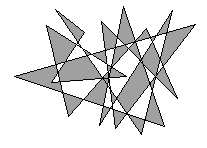
Instead of the four directions, you can do random walks.

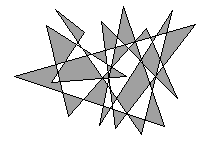
You'll need functions image_load and image_save (and rnd32() for the random walks).
loaderror: ok. thanks for the info.
rrrola: darn cool. if that actually works i will try it. thanks.
rrrola: darn cool. if that actually works i will try it. thanks.
